Literate Programming y Google Code Jam
Índice
1. CodeJam utilizando emacs
Este año han cambiado las normas usuales en el concurso de programación CodeJam de Google.
Antes, cada programador ejecutaba el código localmente, elIgiendo el lenguaje de programación. Ahora, el código se compila y ejecuta en la plataforma del concurso, por lo que la elección de lenguajes está limitada.
Lamentablemente, Scala es mi lenguaje preferido, pero no estaba entre las opciones. Entre las opciones disponibles, elegí refrescar un poco mis conocimientos de C++.
En este momento no tenía ningún IDE para C++ instalado, así que elegí también darle una oportunidad a org-babel, que es una extensión de org-mode que permite ejecutar bloques de código en diferentes lenguajes de programación, e integrarlos dentro de un lenguaje de markup. Al final, se consigue algo parecido a un notebook de Jupyter.
Esta entrada de blog no solo cuenta qué programas hice en la ronda de clasificación, sino que es los programas que usé en la ronda de clasificación (este blog se genera con orgmode)
1.1. source block
Un source block es una parte de un documento org que se considera código fuente de algún lenguaje de programación. Este es un ejemplo de un source block de javascript:
#+begin_src javascript
console.log("Me ejecuto en node!");
#+end_src
Para ejecutarlo, basta con situarse en él y pulsar C-c C-c (en notación, emacs, significa CRLC-C seguido de CTRL-C). La salida estándar del programa se añade al fichero org tras el bloque de código.
Se pueden utilizar varias opciones para controlar cómo se ejecuta:
:results raw replace: Los resultados se escriben tal cual, y la siguiente ejecución reemplaza a los anteriores (en vez de añadirse):cmdline < saving-the-universe.test.in: La entrada estándar del programa será el ficherosaving-the-universe.test.in:wrap EXAMPLE: El resultado se añade al fichero org en un bloque de tipoEXAMPLE.:exports both: Al generar un fichero html o pdf, incluir tanto el source block como el resultadod de la ejecución
Por defecto, el único lenguaje considerado seguro es elisp, pero pueden habilitarse otros muchos. Para habilitar C++ se necesita ejecutar dentro de emacs:
(org-babel-do-load-languages 'org-babel-load-languages '((C . t)))
Por supuesto, esto se hace con un bloque de código que ejecuto con C-c C-c 😄.
2. Saving The Universe Again
Se puede resolver con un algoritmo avaricioso, ya que el mejor cambio posible es siempre la última aparición de la cadena CS (ver la función nextBestChange).
2.1. Solución
#include <iostream>
#include <fstream>
#include <climits>
#include <cstdlib>
#include <string>
using namespace std;
ofstream log("saving-the-universe-again.log");
long value( string p ){
long ret = 0;
long strength = 1;
for( string::iterator i = p.begin() ; i < p.end(); i++ ){
if( *i == 'C' ){
strength *= 2;
}
else{
ret += strength;
}
}
return ret;
}
void swap( string &p, int pos ){
//log << "1swap " << p << endl;
char c = p[pos];
p[pos] = p[pos-1];
p[pos-1] = c;
//log << "2swap " << p << endl;
}
bool nextBestChange( string &p ){
for( int i = p.length()-1 ; i > 0 ; i-- ){
log << i << endl;
if( p[i] == 'S' && p[i-1] == 'C' ){
swap(p,i);
return true;
}
}
return false;
}
long saveTheUniverse( string p, long d ){
long changes = 0;
log << "saveTheUniverse:" << d << ":" << value(p) << endl;
while( value(p) > d ){
if( !nextBestChange(p) ){
log << "IMPOSIBLE" << endl;
return -1;
}
changes++;
}
log << "solucion " << p << " " << d << ":" << changes;
return changes;
}
string output(long l){
if( l == -1)
return "IMPOSSIBLE";
else{
char b[100];
sprintf( b, "%ld", l );
return b;
}
}
int main( int argc, char *argv[] ){
int T;
cin >> T;
for( int i = 0 ; i < T ; i++ ){
long D;
string P;
cin >> D >> P;
log << D << " " << P << endl;
cout << "Case #" << (i+1) << ": " << output(saveTheUniverse(P,D)) << endl;
}
}
Case #1: 1 Case #2: 0 Case #3: IMPOSSIBLE Case #4: 2 Case #5: 0 Case #6: 5
2.2. Problem
An alien robot is threatening the universe, using a beam that will destroy all algorithms knowledge. We have to stop it!
Fortunately, we understand how the robot works. It starts off with a beam with a strength of 1, and it will run a program that is a series of instructions, which will be executed one at a time, in left to right order. Each instruction is of one of the following two types:
- C (for "charge"): Double the beam's strength.
- S (for "shoot"): Shoot the beam, doing damage equal to the beam's current strength.
For example, if the robot's program is SCCSSC, the robot will do the following when the program runs:
- Shoot the beam, doing 1 damage.
- Charge the beam, doubling the beam's strength to 2.
- Charge the beam, doubling the beam's strength to 4.
- Shoot the beam, doing 4 damage.
- Shoot the beam, doing 4 damage.
- Charge the beam, increasing the beam's strength to 8.
In that case, the program would do a total of 9 damage.
The universe's top algorithmists have developed a shield that can withstand a maximum total of D damage. But the robot's current program might do more damage than that when it runs.
The President of the Universe has volunteered to fly into space to hack the robot's program before the robot runs it. The only way the President can hack (without the robot noticing) is by swapping two adjacent instructions. For example, the President could hack the above program once by swapping the third and fourth instructions to make it SCSCSC. This would reduce the total damage to 7. Then, for example, the president could hack the program again to make it SCSSCC, reducing the damage to 5, and so on.
To prevent the robot from getting too suspicious, the President does not want to hack too many times. What is this smallest possible number of hacks which will ensure that the program does no more than D total damage, if it is possible to do so?
2.2.1. Input
The first line of the input gives the number of test cases, T. T test cases follow. Each consists of one line containing an integer D and a string P: the maximum total damage our shield can withstand, and the robot's program.
2.2.2. Output
For each test case, output one line containing Case #x: y, where x is the test case number (starting from 1) and y is either the minimum number of hacks needed to accomplish the goal, or IMPOSSIBLE if it is not possible.
2.2.3. Limits
1 ≤ T ≤ 100. 1 ≤ D ≤ 109. 2 ≤ length of P ≤ 30. Every character in P is either C or S. Time limit: 20 seconds per test set. Memory limit: 1GB.
2.2.4. Sample
Al ejecutar este código (con C-c C-c), se genera el fichero de entrada de prueba.
cat > saving-the-universe.test.in <<EOF 6 1 CS 2 CS 1 SS 6 SCCSSC 2 CC 3 CSCSS EOF
3. Cubic UFO
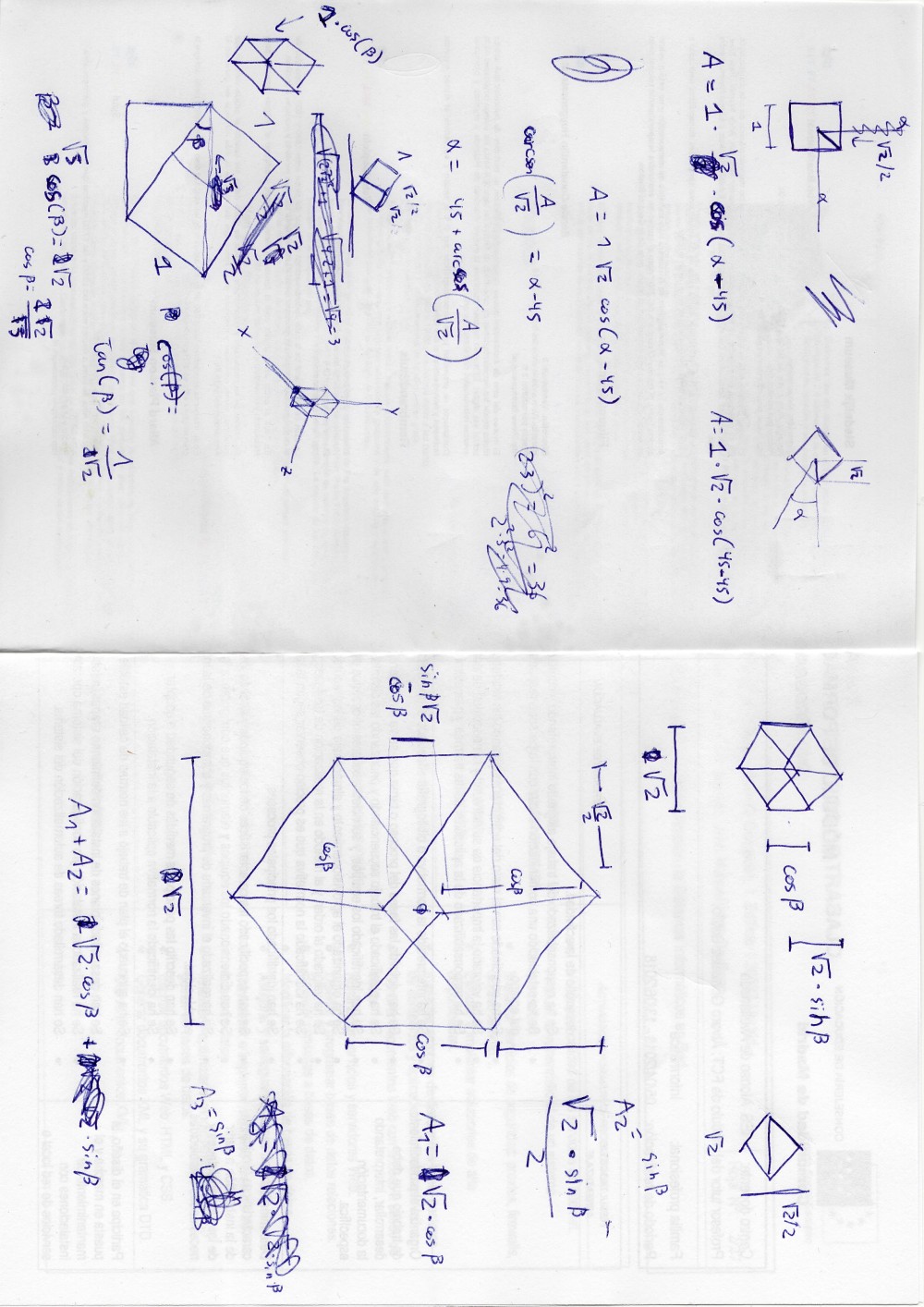
Este es un problema geométrico. Se puede dividir en dos partes
- Si solo se gira un eje, La sombra del cubo es un rectángulo, con la diagonal proyectada. Se puede calcular algebraicamente el ángulo de giro a partir del área (ver la función
onlyAroundX). Con esto, la sombra puede llegar a ser \(\sqrt{2}\). - Si la sombra debe tener un área mayor de \(\sqrt{2}\), se debe girar primero en un eje hasta conseguir un área de \(\sqrt{2}\) (45 grados). Después, se gira en el otro eje para que la sombra sea un hexágono.
- La máxima sombra se da cuando el giro en el segundo eje es de \(arccos(\frac{\sqrt{2}}{\sqrt{3}})\).
- El problema es que no sé calcular algebraicamente el segundo giro a partir del área, pero sí sé calcular el área a partir del ángulo de giro. He utilizado el método de la bisección para encontrar el ángulo a partir del área (función
findAroundZ).
3.1. Solución
Este código lo uso como calculadora de algunas constantes
#include <iostream>
#include <fstream>
#include <climits>
#include <cstdlib>
#include <string>
#include <cmath>
using namespace std;
int main(){
printf( "%lf\n", atan( 1 / (2*sqrt(2)) ) );
printf( "%lf\n", acos( (2*sqrt(2))/3 ) );
}
0.339837 0.339837
Este es el código del problema real
#include <iostream>
#include <fstream>
#include <climits>
#include <cstdlib>
#include <string>
#include <cmath>
using namespace std;
ofstream logger("cubic-ufo.log");
class Mat{
public:
double v[3][3];
Mat(double _v[][3]){
for( int f = 0 ; f < 3 ; f++ ){
for( int c = 0 ; c < 3 ; c++ ){
v[f][c] = _v[f][c];
}
}
}
};
Mat rotX(double a){
double ret[][3] = {
{ 1, 0, 0},
{ 0, cos(a), -sin(a)},
{ 0, sin(a), cos(a) }
};
return Mat(ret);
}
Mat rotZ(double a){
double ret[][3] = {
{ cos(a), -sin(a), 0},
{ sin(a), cos(a),0 },
{0,0,1}
};
return Mat(ret);
}
class Point{
public:
double x,y,z;
Point(double _x, double _y, double _z):x(_x),y(_y),z(_z){}
Point rotate(double aroundX, double aroundZ){
// https://es.mathworks.com/help/phased/ref/rotx.html?requestedDomain=true
Mat rx = rotX(aroundX);
Mat rz = rotZ(aroundZ);
return times(rx).times(rz);
}
Point times(Mat m){
//logger << "\n\n TIMES *******" << endl;
//logger << "this " << toString() << endl;
//logger << m.v[0][0] << "\t" << m.v[0][1] << "\t" << m.v[0][2] << endl;
//logger << m.v[1][0] << "\t" << m.v[1][1] << "\t" << m.v[1][2] << endl;
//logger << m.v[2][0] << "\t" << m.v[2][1] << "\t" << m.v[2][2] << endl;
double retx = x*m.v[0][0] + y*m.v[0][1] + z*m.v[0][2];
double rety = x*m.v[1][0] + y*m.v[1][1] + z*m.v[1][2];
double retz = x*m.v[2][0] + y*m.v[2][1] + z*m.v[2][2];
//logger << "ret " << retx << " " <<rety << " " << retz;
return Point(retx,rety,retz);
}
string toString(){
char b[1000];
snprintf(b, sizeof(b)/sizeof(*b), "%.20lf %.20lf %.20lf", x, y,z );
//////logger << "toString" << " " << x << " " <<y << " " <<z << " " <<b << endl;
return b;
}
};
class Cube{
public:
Point a, b, c;
Cube():a(0.5,0,0), b(0,0.5,0), c(0,0,0.5){}
Cube rotate(double aroundX, double aroundZ ){
Cube ret;
ret.a = a.rotate(aroundX,aroundZ);
ret.b = b.rotate(aroundX,aroundZ);
ret.c = c.rotate(aroundX,aroundZ);
//logger << "rotate " << toString() << endl;
return ret;
}
string toString(){
char buf[1000];
snprintf(buf, sizeof(buf)/sizeof(*buf), "%s \n%s \n%s", a.toString().c_str(), b.toString().c_str(), c.toString().c_str() );
return string(buf);
}
};
const double maxAroundZ = acos( sqrt(2)/sqrt(3) );
const double SQRT2 = sqrt(2);
Cube onlyAroundX( double a ){
double aroundX = M_PI/4 + acos( a/SQRT2 );
return Cube().rotate(aroundX,0);
}
double maxAreaForAroundZ(double aroundz){
return SQRT2*cos(aroundz) + sin(aroundz);
}
double findAroundZ(double a){
double minz = 0;
double maxz = maxAroundZ;
double ret = (maxz + minz)/2;
double area = maxAreaForAroundZ(ret);
while( fabs( area - a) > 0.00000001 ){
if( area > a )
maxz = ret;
else
minz = ret;
ret = (maxz + minz)/2;
area = maxAreaForAroundZ(ret);
}
return ret;
}
int main( int argc, char *argv[] ){
int T;
cin >> T;
for( int i = 0 ; i < T ; i++ ){
double A;
cin >> A;
if( A <= SQRT2){
Cube c = onlyAroundX(A);
printf( "Case #%d:\n%s\n", i+1, c.toString().c_str() );
}
else{
Cube c = onlyAroundX(SQRT2).rotate(0,findAroundZ(A));
printf( "Case #%d:\n%s\n", i+1, c.toString().c_str() );
}
}
}
Case #1: 0.50000000000000000000 0.00000000000000000000 0.00000000000000000000 0.00000000000000000000 0.00000000000000003062 0.50000000000000000000 0.00000000000000000000 -0.50000000000000000000 0.00000000000000003062 Case #2: 0.50000000000000000000 0.00000000000000000000 0.00000000000000000000 0.00000000000000000000 0.35355339059327378637 0.35355339059327373086 0.00000000000000000000 -0.35355339059327373086 0.35355339059327378637 Case #3: 0.49789095814646988636 0.04587585199198114527 0.00000000000000000000 -0.03243912603624025254 0.35206207279683637834 0.35355339059327373086 0.03243912603624025254 -0.35206207279683632283 0.35355339059327378637
3.2. Problem
A mysterious cubic alien ship has appeared in the sky over Toronto! In this problem, Toronto is a plane in three-dimensional space that is parallel to the xz plane at y = -3 km. The alien ship is a solid cube with side length 1 km, centered at (0 km, 0 km, 0 km), with its eight corners at (+/- 0.5 km, +/- 0.5 km, +/- 0.5 km). The ship is casting an ominous shadow onto the plane; formally, the shadow is the orthogonal projection of the cube onto the plane. (We consider the sun to be a point infinitely far above the Toronto plane along the y-axis.)
The military is willing to tolerate the ship as long as the aliens meet their bureaucratic demand: the shadow must cover an area of the plane that is acceptably close to A km2 (see the Output section for a precise definition). They have hired you, a geometric linguistics expert, to convey this demand to the aliens. In your communications so far, you have learned that the ship cannot change size, and the center of the ship cannot move, but the ship is able to rotate arbitrarily in place.
Please find a way that the aliens can rotate the ship so that the shadow's area is close to A. Express your rotation using three points: the centers of any three non-pairwise-opposing faces.
3.2.1. Input
The first line of the input gives the number of test cases, T. T test cases follow; each consists of one line with a rational A, the desired area of the shadow, in km2, with exactly six digits after the decimal point.
It is guaranteed that there is always a way to rotate the ship in the desired manner for the values of A allowed in this problem.
3.2.2. Output
For each test case, first output one line containing Case #x:, where x is the test case number (starting from 1). Then, output three more lines with three rational values each: the x, y, and z coordinates of one of your three provided face-centers, as described above. You are welcome to use decimal (e.g., 0.000123456) or scientific notation (e.g., 1.23456e-4).
Your answer will be considered correct if and only if all of the following are true:
- The distance (in km) from each point to the origin must be between 0.5 - 10-6 and 0.5 + 10-6, inclusive.
- The angles (in radians) between segments connecting the origin to each point must be between π/2 - 10-6 and π/2 + 10-6, inclusive.
- The area of the shadow (in km2), computed by projecting all 8 vertices onto the y = -3 plane and finding the area of the convex hull of those projected points, must be between A - 10-6 and A + 10-6, inclusive. We will compute the vertices as +/- p1 +/- p2 +/- p3 (that is, for each pi we add either pi or -pi to the total using vector addition), where p1, p2, and p3 are the face-centers that you provide.
Please note that you might need to output more than 6 digits after the decimal point to safely pass the checks mentioned above. If there are multiple acceptable answers, you may output any one of them.
3.2.3. Limits
1 ≤ T ≤ 100. Time limit: 30 seconds per test set. Memory limit: 1GB.
Test set 1 (Visible) 1.000000 ≤ A ≤ 1.414213
Test set 2 (Hidden) 1.000000 ≤ A ≤ 1.732050
3.2.4. Sample
Al ejecutar este código (con C-c C-c), se genera el fichero de entrada de prueba.
cat > cubic-ufo.test.in <<EOF 3 1.000000 1.414213562373095048801688724209698078569671875376948073176679737990732478462107038850387534327641573 1.5 EOF
