Capa de enlace
Índice
1. Introducción
1.1. La capa de enlace
- Es la capa 2 de la arquitectura OSI.
- Se encarga de conseguir que la comunicación de datos se produzca correctamente a través de un medio físico de transmisión.
- Para lograr que dos dispositivos adyacentes se comuniquen, se necesita un control del intercambio de datos: el control del enlace.
- La capa de enlace proporciona a la capa de Red un servicio de transporte de bits fiable (asegura que los bit se trasmiten correctamente por el medio físico).
- El bloque de datos transmitido se denomina TRAMA.
1.2. Funciones de la capa de enlace
- Sincronización a nivel de trama.
- Control de flujo: las estaciones deben ponerse de acuerdo en el ritmo de trasmisión de datos.
- Control de errores: los enlaces no son perfectos. Hay que controlar que no haya errores en la transmisión.
- Direccionamiento: si hay varios posibles destinos, es necesario identificar a quien va dirigida la trama.
- Gestión del enlace:
- Inicio de la transmisión
- Mantenimiento de la transmisión
- Finalización de la transmisión
1.3. MAC y LLC
- En la arquitectura IEEE 802, el nivel de enlace se divide en dos subcapas:
- LLC: se encarga de las funciones comunes de la capa independientemente del medio físico usado
- Control de errores
- Direccionamiento
- Sus funciones han sido definidas por el subgrupo 802.2.
- MAC: se encarga del acceso al medio (gestión del enlace)
- LLC: se encarga de las funciones comunes de la capa independientemente del medio físico usado
2. Tramas
- Una trama es un bloque de bits agrupados que son enviados por la línea.
- El tamaño de la trama depende del tipo de red.
- Agrupar los bits en tramas facilita:
- la detección y corrección de errores
- la compartición del medio.
- Una trama se compone de tres partes
- Información sobre la trama
- Datos.
- Redundancia.
3. Control de flujo
- Veremos el control de flujo cuando estudiemos TCP
- Algunos protocolos de nivel 2 lo soportan. No es el caso de Ethernet.
4. Acceso al medio
4.1. Clasificación general
- Medio repartido
- FDM: multiplexación en frecuencias
- Cada vez menos usado: se puede infrautilizar el ancho de banda
- TDM: multiplexación en tiempo
- FDM: multiplexación en frecuencias
- Medio compartido
- Sin colisiones
- Sondeo
- Paso de testigo (Token Bus)
- Con colisiones
- CSMA/CD (Ethernet)
- CSMA/CA (Wifi)
- Sin colisiones
4.2. FDM
- Se multiplexa el canal por frecuencia
- Cada canal se asigna a un nodo de la red
- Usado en:
- Red telefónica (analógica)
- Radio FM/AM
- DSL
4.3. TDM
- Se multiplexa el canal por tiempo (a la Round Robin)
- Cada canal se asigna a un nodo de la red
- Más común en transmisiones digitales
- GSM
- SONET
4.4. Paso de testigo
- Cada nodo debe esperar a tener el turno de emisión
- El turno se utiliza, y se cede al siguiente por un testigo
- Un mensaje especial que indica que no se quiere emitir más
- Y señala el siguiente equipo que emitirá
- Ejemplos:
4.5. CSMA/CD
- Carrier-sense multiple access with collision detection
- Multiple access: Cualquiera puede emitir usando el mismo medio
- Carrier-sense: Antes de emitir, se comprueba que nadie más esté emitiendo
- Collision detection:
- Durante la transmisión, detecto si otro también emite
- Si se produce una colisión, dejo de emitir
- Y espero un tiempo aleatorio para volver a intentarlo

Figura 1: Animación de una colisión en un bus
4.6. CSMA/CA
- Carrier-sense multiple access with collision avoidance
- Similar a CSMA/CD
- Collision avoidance para evitar los nodos ocultos:
- Antes de emitir los datos se envía un RTS (request to send)
- Es un mensaje pequeño, con poca probalibilidad de colisión
- Un nodo central recibe los RTS y determina quién recibe un CTS (clear to send)
- El que recibe el CTS puede enviar sus datos sin problemas
- Antes de emitir los datos se envía un RTS (request to send)
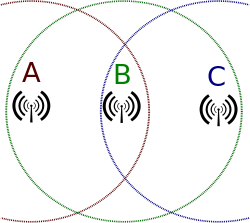
Figura 2: Los nodos de los extremos están ocultos entre sí, aunque el central detecta a los dos
5. Control de errores
- Consiste en enviar algunos bits añadidos a los datos con información que permita detectar o corregir los errores.
- El porcentaje de redundancia se calcula como \[\frac{bitsdecontrol}{bitstotales}\times 100\]
- Los errores pueden
- Detectarse
- Adicionalmente, corregirse
5.1. Errores
- Un único bit
- Más comunes en transmisión en paralelo
- Ráfagas de bits
- Una interferencia actúa sobre los medios de transmisión
- Perturban varios bits seguidos
- Afectan más a comunicaciones en serie
5.2. Detección de errores
- ECO
- El receptor envía una copia exacta de la información recibida al emisor.
- El emisor confirma con otra trama que la información es correcta
- Paridad lineal. Se añade un bit extra, indicando si el número de bits con valor a 1 es par o impar.
100100, con paridad par, se envía como1001000100100, con paridad impar, se envía como1001001- Problema: ¿Qué pasa si cambia un número par de bits?
5.2.1. Paridad de bloque
- Paridad de bloque. Se distribuyen los datos en una tabla y se calcula paridad por cada línea y columna.
- Mensaje:
1100101011011010110101001111011100111001111010000, con paridad par - Se envía
1100101001101100101101001001111101110010110011111010000010010000
- Mensaje:
| Datos | Paridad lineal | |
|---|---|---|
| 1100101 | 0 | |
| 0110110 | 0 | |
| 1011010 | 0 | |
| 1001111 | 1 | |
| 0111001 | 0 | |
| 1100111 | 1 | |
| 1010000 | 0 | |
| Paridad de bloque | 1001000 | 0 |
| Datos | Paridad lineal | |
|---|---|---|
| 1100 0 01 | 0 | |
| 0110 1 10 | 0 | |
| 1011 0 10 | 0 | |
| 1001 1 11 | 1 | |
| 0111 0 01 | 0 | |
| 1100 1 11 | 1 | |
| 1010 0 00 | 0 | |
| Paridad de bloque | 1001 0 00 | 0 |
| Datos | Paridad lineal | |
|---|---|---|
| 1 100 0 01 | 0 | |
| 0 110 1 10 | 0 | |
| 1 011 0 10 | 0 | |
| 1 001 1 11 | 1 | |
| 0 111 0 01 | 0 | |
| 1 100 1 11 | 1 | |
| 1 010 0 00 | 0 | |
| Paridad de bloque | 0 001 0 00 | 0 |
- Conclusión:
- Si falla un bit, puedo arreglarlo
- Si fallan dos bits, lo detecto
- Si fallan más,
- Puedo no enterarme
- Puede parecer que ha fallado solo uno
- Puedo detectar el error
5.3. Actividad
- Calcular la paridad bidimensional del siguiente mensaje:
1001101, 1111010, 1100110, 1110001, 1101001, 1110111, 0010111
5.4. Distancia de Hamming
- Cuando se produce un error, cambian algunos bits
- Según la codificación utilizada, no todas las combinaciones de 0s y 1s son posibles
- Ejemplo: 4B/5B
- La distancia de Hamming de un código es la cantidad de bits que hay que cambiar en una combinación válida para llegar a otra combinación válida
- Cuanto mayor sea la distancia, más robusto es el código frente a errores
- Si la distancia es \(d\), se pueden detectar errores de hasta \(d-1\) bits.
- Si la distancia es \(d\), se pueden corregir errores de hasta \(\lfloor(d-1)/2\rfloor\) bits.
- ¿Cuál es la distancia de Hamming de una transmisión con paridad?
5.5. CRC
- Al principio de la comunicación, emisor y receptor acuerdan un Polinomio Generador.
- Al iniciar la transmisión se añaden un número predeterminado de ceros a la información a enviar y se divide utilizando el polinomio generador.
- El receptor realiza nuevamente una división sobre los datos recibidos y si el resto es 0 indica que la trama se ha recibido sin errores.
- Finalmente se descartan los bits añadidos en el transmisor para quedarnos con el mensaje original.
5.5.1. ¿Por qué CRC?
- Hay versiones de CRC para diferentes longitudes de polinomio: CRC16, CRC32,…
- Los errores se producen típicamente a ráfagas
- Para un CRC de \(n\) bits
- Se detectan todos los errores de ráfagas de menos de \(n\) bits incorrectos
- Se detecta una fracción de las ráfagas más largas (\(1 - 2^{-n}\))
| Longitud de crc | Porcentaje de detección de ráfagas mayores |
|---|---|
| 8 | 99.609375 |
| 16 | 99.998474 |
| 32 | 99.9999999767169 |
6. Corrección de errores
- La detección de errores es el primer paso
- Una vez detectado:
- Se puede ignorar (las capas más altas deben arreglar el error)
- Se puede corregir
- Ethernet no corrige errores, pero veremos algunas técnicas que pueden usar otras capas 2
6.1. Retransmisión
- Es el método de corrección más sencillo.
- Se detecta el error y se pide al emisor que vuelva a enviar la trama.
- Se tienen que memorizar las tramas enviadas hasta la recepción de un ACK que confirme que el envío de información fue exitosa.
6.2. Corrección: Código Hamming
- Codificación que permite la detección y la corrección de un bit
- Tienen distancia 3
- Se inluyen bits de paridad de la siguiente forma:
- Los bits de las posiciones \(s=2^{p-1}\) son de paridad: 1, 2, 4, 8…
- El resto son de datos
- El bit de la posición \(s\) se incluye en el bit de paridad \(p\) si la expresión de \(s\) en binario tiene a 1 el bit \(p\)
| p1 | p2 | d1 | p3 | d2 | d3 | d4 | p4 | d5 | d6 | d7 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| s1 | s2 | s3 | s4 | s5 | s6 | s7 | s8 | s9 | s10 | s11 | |
| p1 | x | x | x | x | x | x | |||||
| p2 | x | x | x | x | x | x | |||||
| p3 | x | x | x | x | |||||||
| p4 | x | x | x | x |
6.2.1. Clasificación de códigos de Hamming
- La tabla anterior se puede hacer para cualquier longitud
- El ejemplo tiene 11 bits en total, 7 son de datos: Hamming(11,7)
- También es común el Hamming(7,4)
| Datos | Hamming |
|---|---|
| 0000 | 0000000 |
| 1000 | 1110000 |
| 0100 | 1001100 |
| 1100 | 0111100 |
| 0010 | 0101010 |
| 1010 | 1011010 |
| 0110 | 1100110 |
| 1110 | 0010110 |
| 0001 | 1101001 |
| 1001 | 0011001 |
| 0101 | 0100101 |
| 1101 | 1010101 |
| 0011 | 1000011 |
| 1011 | 0110011 |
| 0111 | 0001111 |
| 1111 | 1111111 |
6.2.2. Ejemplo Hamming(11,7)
Para transmitir
0110101p1 p2 d1 p3 d2 d3 d4 p4 d5 d6 d7 s1 s2 s3 s4 s5 s6 s7 s8 s9 s10 s11 Datos 0 1 1 0 1 0 1 p1 0 1 0 1 1 p2 0 1 0 0 1 p3 1 1 0 p4 1 0 1
- Para transmitir
0110101 Se transmite
10001100101p1 p2 d1 p3 d2 d3 d4 p4 d5 d6 d7 s1 s2 s3 s4 s5 s6 s7 s8 s9 s10 s11 Datos 0 1 1 0 1 0 1 p1 1 0 1 0 1 1 p2 0 0 1 0 0 1 p3 0 1 1 0 p4 0 1 0 1 Datos (con paridad): 1 0 0 0 1 1 0 0 1 0 1
6.2.3. Detección de un error con Hamming
- Se recibe
11001100101
| p1 | p2 | d1 | p3 | d2 | d3 | d4 | p4 | d5 | d6 | d7 | Paridad | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| s1 | s2 | s3 | s4 | s5 | s6 | s7 | s8 | s9 | s10 | s11 | ||
| Recibida: | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | |
| p1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | |||||
| p2 | 1 | 0 | 1 | 0 | 0 | 1 | 1 (error) | |||||
| p3 | 0 | 1 | 1 | 0 | 0 | |||||||
| p4 | 0 | 1 | 0 | 1 | 0 |
- Hay un error, y se localiza en la posición
0010: s2 (p2)
6.2.4. Ejercicio
- Decide si las siguientes palabras de código Hamming son correctas. Si no son correctas, corrígelas.
100011001010010011001001110111001
6.2.5. ¿Y si hay más de 1 error?
- Su distancia de Hamming es 3, así que no se puede corregir
- En Hamming extendido se añade un bit de paridad adicional
- Permite detectar errores de tres bits, pero no corregirlos
6.3. Ejercicio
- Calcula el porcentaje de redundancia de:
- Tramas de 1000 bytes, con crc32 incluido en los 1000 bytes
- Tramas de 100 bytes, con crc16 añadido a los 100 bytes
- Hamming (7,4)
- Hamming (11,7)
- Hamming (11,7) extendido
- Paridad lineal: un bit de paridad cada 7 de datos
- Paridad de bloque: un bit de paridad lineal cada 7 de datos, bloques de 49 bits de datos
6.4. Códigos Reed Solomon
- En la actualidad, Hamming tiene una utilidad didáctica más que práctica
- En la actualidad se utiliza Reed-Solomon
- CD, DVD, BlueRay
- QR (generador)
- Raid 6
- DVB, WiMax, transmisiones aeroespaciales
7. Ejemplo: RS232
- Conocido como puerto serie
- Utiliza codificación de canal NRZ
- Siempre hay un bit de inicio de palabra, a nivel alto
- Parámetros:
- baudios
- bits de datos: generalmente 8
- bit de paridad: sin paridad, paridad par o paridad impar
- bits de parada: 1 o 2, nivel bajo

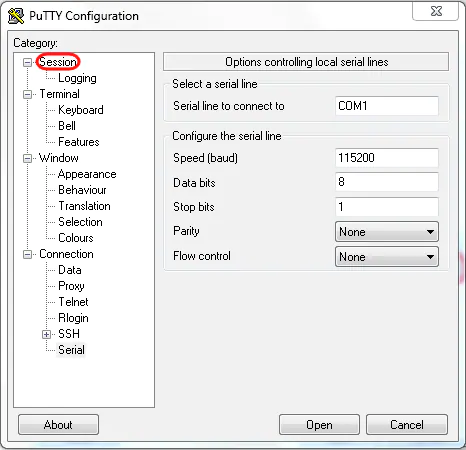
Ejemplo: rootear dispositos
8. Referencias
- Formatos:
- Alojado en Github